백준 1260번. DFS와 BFS (C++)

< 문제 >

문제

그래프를 DFS로 탐색한 결과와 BFS로 탐색한 결과를 출력하는 프로그램을 작성하시오. 단, 방문할 수 있는 정점이 여러 개인 경우에는 정점 번호가 작은 것을 먼저 방문하고, 더 이상 방문할 수 있는 점이 없는 경우 종료한다. 정점 번호는 1번부터 N번까지이다.

 

입력

첫째 줄에 정점의 개수 N(1 ≤ N ≤ 1,000), 간선의 개수 M(1 ≤ M ≤ 10,000), 탐색을 시작할 정점의 번호 V가 주어진다. 다음 M개의 줄에는 간선이 연결하는 두 정점의 번호가 주어진다. 어떤 두 정점 사이에 여러 개의 간선이 있을 수 있다. 입력으로 주어지는 간선은 양방향이다.

 

출력

첫째 줄에 DFS를 수행한 결과를, 그 다음 줄에는 BFS를 수행한 결과를 출력한다. V부터 방문된 점을 순서대로 출력하면 된다.

 

예제 입력

 

<해설>

위 문제는, DFS와 BFS의 이론 그자체를 묻고 있는 문제다.

DFS, BFS는 그래프 탐색 알고리즘으로, 모든 노드를 방문하여 경로를 탐색하는 알고리즘으로 가장 기초적인 알고리즘이다.

DFS는 재귀 혹은 스택, BFS는 큐를 사용하여 탐색할 수 있다.

여기서는 DFS는 재귀, BFS는 큐로 해설해보도록 한다.

 

- 풀이 과정 (예제 입력 1번을 예시로 한다.)

먼저, C++의 벡터를 활용한다. 노드들을 저장해 둘 이중 벡터와, 노드가 방문했는지 여부를 체크하기 위한 visited 배열을 선언한다.

이중 벡터로 선언하는 이유는 각 노드에 연결 되어 있는 노드들을 저장하기 위해서이다. 

vector< vector<int> > adj;
vector<bool> visited;

 

 

선언을 하였으니, 값을 저장해주어야 한다. 백준에서 요구한대로 값을 입력받고 저장해보자.

 

1. "첫째 줄에 정점의 개수 N(1 ≤ N ≤ 1,000), 간선의 개수 M(1 ≤ M ≤ 10,000), 탐색을 시작할 정점의 번호 V가 주어진다."가 조건이었으므로, 정점의 개수 node, 간선의 개수 edge, 탐색을 시작할 정점 start를 cin으로 입력받는다.

2. assign 함수를 활용하여 vector에 node만큼 -1로 채워진 벡터를 삽입한다. 그리고 visited 벡터도, adj의 size만큼 false로 초기화를 시켜준다. (node "만큼" 할당되므로, index는 0으로 시작한다.)

3. 그리고 edge, 간선의 개수만큼 for문을 돌면서 연결되어 있는 노드를 삽입해준다. 이 때, 각 노드는 쌍방향으로 연결되어 있으므로, 각 노드의 index에 서로 바꿔가면서 넣어준다.

4. 그리고 node 개수만큼 for문을 돌면서 adj의 원소로 들어가있는 vector를 sort해준다. (뒤에서 for문을 돌기 위함)

 

 

int main() {
  int node;
  int edge;
  int start;
  cin >> node >> edge >> start;

  adj.assign(node, vector<int>(1, -1));
  visited = vector<bool>(adj.size(), false);

  for (int i = 0; i < edge; i++) {
    int pair1, pair2;
    cin >> pair1 >> pair2;    
    adj[pair1 - 1].push_back(pair2 - 1);
    adj[pair2 - 1].push_back(pair1 - 1);
  }

  for (int i = 0; i < node; i++) {
    sort(adj[i].begin(), adj[i].end());
  }

 

5. dfs 함수를 선언해서 start (첫 정점)을 파라미터로 넘겨주고 호출한다.

6. dfs가 끝나고 난 후, visited 벡터의 원소를 모두 false로 초기화 해준다.

7. bfs 함수를 선언해서 start (첫 정점)을 파라미터로 넘겨주고 호출한다.

 

 

  dfs(start - 1);
  cout << endl;

  visited = vector<bool>(adj.size(), false);
  bfs(start - 1);

  return 0;
}

 

이제 dfs함수와 bfs함수를 정의해보자. 먼저 dfs부터 보자.

dfs에서는 기본적으로, dfs함수가 호출된 것 = 노드를 방문한 것 이다.

1. 따라서, "방문된 점을 순서대로 출력하면 된다." 이므로 dfs함수에 진입하자마자 here + 1을 출력해준다. (here는 0부터 시작되는 index값으로 들어올 것이므로)

2. 방문을 한 노드이므로 visited의 here index는 true로 변경해준다.

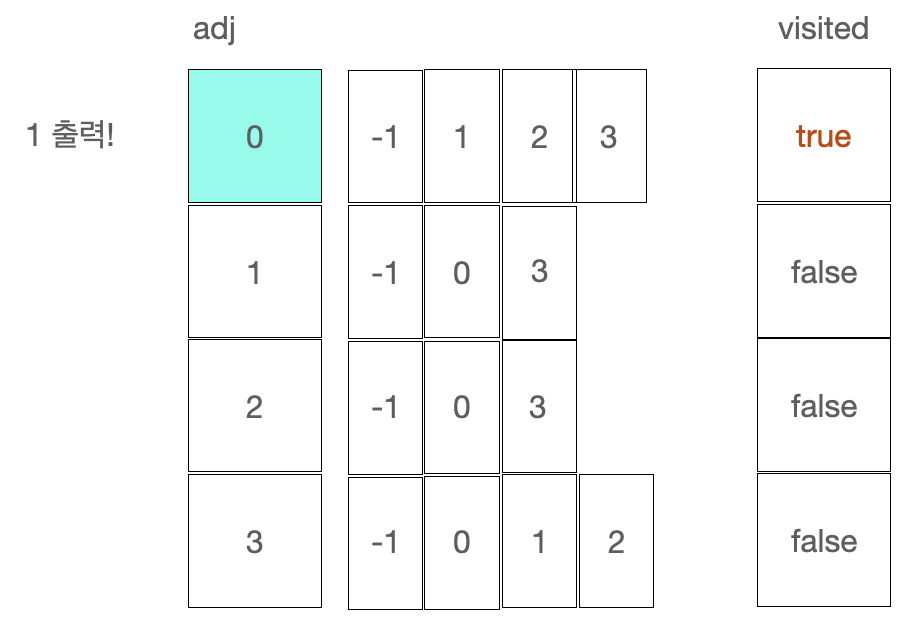
3. adj[here]를 for문을 돌면서 노드를 탐색한다. 이 때, adj[here][i]가 -1이면 자기 자신이기 때문에, 건너 뛰고, visited가 true인 경우에는 이미 방문한 노드이기 때문에, visited가 false일 때만 재귀로 dfs 함수를 호출해주도록 한다.

 

 

void dfs(int here) {
  cout << here + 1 << " ";
  visited[here] = true;

  for (int i = 0; i < adj[here].size(); i++) {
    int there = adj[here][i];
    if (there == -1) continue;
    if (!visited[there]) {
      dfs(there);
    }
  }
}

 

bfs도 비슷한 맥락이다.

그러나 bfs는 dfs처럼 함수가 호출됐을 때가 노드에 방문한 시점이 아니다. dfs는 재귀 "함수"를 통해 탐색하였기 때문에 가능하였지만, bfs는 큐에 값을 넣는 시점이 노드에 방문한 시점이다.

1. 우선 처음 정점으로 들어온 here를 큐에 넣고, 큐에 넣었으므로 노드에 방문한 것이다. 따라서 visited[here] 는 true로 바꿔준다.

2. 1을 통해 큐를 초기화하였고, 큐가 비어서 데이터가 없을 때 까지 반복문을 돈다.

3. 반복문에 진입하면, 큐에 가장 앞에 있는 원소에 1을 더한 값을 출력해주면서 해당 원소를 pop으로 빼준다.

4. adj에서 방금 큐에서 빠진 원소를 index로 갖는 벡터를 for문을 돌면서 탐색해준다.

5. 해당 벡터에서 dfs와 마찬가지로 원소가 -1이 아니고 visited가 false인 원소일 경우, 큐에 넣어주고 visited를 true로 바꿔준다.

 

 

void bfs(int here) {
  queue < int > q;
  q.push(here);
  visited[here] = true;

  while(!q.empty()) {
    int start = q.front();
    cout << start  + 1 << " ";
    q.pop();

    for (int j = 0; j < adj[start].size(); j++) {
      int there = adj[start][j];
      if (there == -1) continue;
      if (!visited[there]) {
        q.push(there);
        visited[there] = true;
      }
    }
  }
}

 

최종 코드는 다음과 같다.

#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>

using namespace std;

vector< vector<int> > adj;
vector<bool> visited;

void dfs(int here) {
  cout << here + 1 << " ";
  visited[here] = true;

  for (int i = 0; i < adj[here].size(); i++) {
    int there = adj[here][i];
    if (there == -1) continue;
    if (!visited[there]) {
      dfs(there);
    }
  }
}

void bfs(int here) {
  queue < int > q;
  q.push(here);
  visited[here] = true;

  while(!q.empty()) {
    int start = q.front();
    cout << start  + 1 << " ";
    q.pop();

    for (int j = 0; j < adj[start].size(); j++) {
      int there = adj[start][j];
      if (there == -1) continue;
      if (!visited[there]) {
        q.push(there);
        visited[there] = true;
      }
    }
  }
}

int main() {
  int node;
  int edge;
  int start;
  cin >> node >> edge >> start;

  adj.assign(node, vector<int>(1, -1));
  visited = vector<bool>(adj.size(), false);

  for (int i = 0; i < edge; i++) {
    int pair1, pair2;
    cin >> pair1 >> pair2;    
    adj[pair1 - 1].push_back(pair2 - 1);
    adj[pair2 - 1].push_back(pair1 - 1);
  }

  for (int i = 0; i < node; i++) {
    sort(adj[i].begin(), adj[i].end());
  }

  dfs(start - 1);
  cout << endl;

  visited = vector<bool>(adj.size(), false);
  bfs(start - 1);

  return 0;
}

 

좀 예전에 풀었던 문제인데, 지금보니까 굳이 sort를 하지 않고도 할 수 있는 방법이 있을 것 같다. (그리고 애초에 순서대로 삽입될 듯 하다....)

C++은 뭔가 라이브러리나 내장 모듈 사용이 자유롭지(?) 않다는 생각이 들어서 그렇게 했던 것 같기도 하다.

좀 더 효율적으로 짤 수 있는 방안을 생각해보긴 해야겠다.